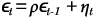Errata for Introduction to Time Series Using Stata
The errata for Introduction to Time Series Using Stata are provided below. Click here for an explanation of how to read an erratum. Click here to learn how to determine the printing number of a book.
| (1) | Chapter 1, p. 43, scatter command |
|---|
|
. scatter gnppcap girlstoboys if year==2007, > yscale(log) xlabel(60 70 80 90 100 110) > ylabel(100 1000 10000 100000) |
. scatter gnppcap girlstoboys if year==2007 > [fw=int(pop + 0.5)], > yscale(log) xlabel(60 70 80 90 100 110) > ylabel(100 1000 10000 100000) |
| (1), (2) | Chapter 1, p. 69, third line of third paragraph |
|---|
| ...S.y, is the same as y - L4.y. | ...S4.y, is the same as y - L4.y. |
| (1) | Chapter 2, p. 73, first equation |
|---|
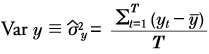
|
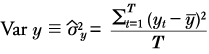
|
| (1) | Chapter 2, p. 74, second line of third paragraph |
|---|
| ...choose Ha (H0) if .... | ...choose Ha (reject H0) if ... |
| (1), (2) | Chapter 2, p. 82, second expression on second line of second paragraph |
|---|
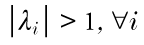
|
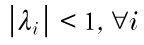
|
| (1), (2) | Chapter 2, p. 82, expression on third line of second paragraph |
|---|
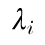
|
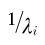
|
| (1) | Chapter 4, p. 161, tsline command |
|---|
| . tsline currcomp date if year>1997, ytitle($ billions) | . tsline currcomp if year>1997, ytitle($ billions) |
| (1), (2) | Chapter 5, p. 180, do-file example |
|---|
|
. generate epsilon = eta in f (119 missing values generated) |
The first observation in a time series typically requires special treatment.
In this simulation, the first value of εt should be drawn from the stationary
distribution of εt. Because
where ηt follows a standard normal distribution, the stationary distribution of εt is N{0, 1/(1 - ρ2)}. The appropriate command to draw the first value of εt is
. generate epsilon = rnormal() * sqrt(1/0.19) in f This shortcut—that is, drawing the first observation of the disturbance from a standard normal distribution instead of the stationary distribution—occurs in several examples in this book. However, the impact of this shortcut is slight in these examples. In the example on pages 180–181, the correlation between the shortcut and the corrected versions of εt is 0.9978, and the corrected version generates no significant changes in the results. |
| (1), (2) | Chapter 5, p. 182, footnote 11. |
|---|
| For the purposes of this example, we take advantage of our knowledge that the errors in this equation do not exhibit higher-order autocorrelation. In the real world, we would have to allow for this possibility. In later chapters, we take some pains to determine the correct number of lags to include. |
In fact, the errors do exhibit higher-order autocorrelation even though
the error process in this example is called first-order autocorrelation. The
footnote confuses the order of the error process (firstorder) with the
number of significant autocorrelations of εt. The newey command in the
example should include a high number of lags to account for these autocorrelations. For instance,
. newey y x, lag(20) works well in this example. |
| (1), (2) | Chapter 5, p. 183, first sentence following the equations |
|---|
| The disturbances in this new regression are serially uncorrelated, so least-squares estimates are unbiased and errorscient. | The disturbances in this new regression are serially uncorrelated, so least-squares estimates of the starred statistics are unbiased and efficient. However, OLS does not provide efficient estimates of the fundamental (unstarred) parameters, which are nonlinear functions of the starred parameters. |
| (1) | Chapter 5, p. 255, do-file example of wntestq |
|---|
|
. wntestq resid Portmanteau test for white noise -------------------------------- Portmanteau (Q) statistic = 41.3526 Prob > chi2(40) = 0.4114 |
The degrees of freedom in this χ2 test should be adjusted for the ARMA
parameters estimated by the arima command. The wntestq command does
not provide an option for adjusting the degrees of freedom in the test, but
the correct p-value can be displayed by typing
. display chi2tail(38,41.3526) |
| (1) | Chapter 6, p. 202, third equation |
|---|
| \[ E\epsilon_t\epsilon_{t-j}, \forall j \neq 0 \] | \[ E\epsilon_t\epsilon_{t-j}=0, \forall j \neq 0 \] |
| (1) | Chapter 7, p. 268, after the first displayed equation |
|---|
| the trend is... | the mean (there is no trend) is... |
| (1) | Chapter 9, p. 300, last displayed equation |
|---|
| \[{\boldsymbol \mu} = \left[ \begin{array}{c} \mu_1 \\ \mu_2 \\ \vdots \\ \mu_p \\ \end{array} \right] \] | \[ {\boldsymbol \mu} = \left[ \begin{array}{c} \mu_1 \\ \mu_2 \\ \vdots \\ \mu_n \\ \end{array} \right] \] |
| (1) | Chapter 9, p. 301, second displayed equation |
|---|
| \[ {\boldsymbol \epsilon}_t = \left[ \begin{array}{c} \epsilon_1 \\ \epsilon_2 \\ \vdots \\ \epsilon_p \\ \end{array} \right] \] | \[ {\boldsymbol \epsilon}_t = \left[ \begin{array}{c} \epsilon_{1,t} \\ \epsilon_{2,t} \\ \vdots \\ \epsilon_{n,t} \\ \end{array} \right] \] |
| (1) | Chapter 9, p. 331, footnote 25 |
|---|
| To convince yourself of these statements, consider the two-equation system \[ \begin{eqnarray*} y_t & = & \alpha_{11} y_{t-1} + \alpha_{12} x_{t-1} + \epsilon_{1,t} \\ x_t & = & \alpha_22 x_{t-1} + \epsilon_{2,t} \end{eqnarray*} \] It's straightforward to show \[ \begin{eqnarray*} \gamma_{yx}(1) & = & {\alpha_{11}\alpha{22} \over 1 - \alpha_{11}\alpha{22}} \gamma_{xx}(1) \\ & \neq & \alpha_{11}\alpha_{22}\gamma_{yx}(0) + \alpha_{12}\alpha_{22}\gamma_{xx}(0) \\ & = & \gamma_{yx}(-1) \end{eqnarray*} \] and \[ \gamma_{yx}(1) = \gamma_{xy}(-1) \] | To convince yourself of these statements, consider the two-equation system \[ \begin{eqnarray*} y_t & = & \alpha_{11} y_{t-1} + \alpha_{12} x_{t-1} + \epsilon_{1,t} \\ x_t & = & \alpha_{22} x_{t-1} + \epsilon_{2,t} \end{eqnarray*} \] It's straightforward to show \[ \begin{eqnarray*} \gamma_{yx}(1) & = & {\alpha_{11}\alpha_{22} \over 1 - \alpha_{11}\alpha_{22}} \gamma_{xx}(1) \\ & \neq & \alpha_{11}\alpha_{22}\gamma_{yx}(0) + \alpha_{12} \alpha_{22}\gamma_{xx}(0) \\ & = & \gamma_{yx}(-1) \end{eqnarray*} \] and \[ \gamma_{yx}(1) = \gamma_{xy}(-1) \] |
| (1) | Chapter 9, p. 339, first displayed equation |
|---|
| \[ y_t = \mu + \phi_i y_{t-1} + \cdots + \phi_p y_{t-p} + \epsilon_t \] | \[ y_t = \mu + \phi_1 y_{t-1} + \cdots + \phi_p y_{t-p} + \epsilon_t \] |
| (1), (2) | Chapter 9, p. 339, third displayed equation |
|---|
| \begin{eqnarray*} y_{t-k } - \nu & = & \psi_{t-k} \\ y_{t-k-1} - \nu & = & \psi_{t-k-1} \\ \vdots & \vdots & \vdots \\ y_{t} - \nu & = & \psi_{t} \end{eqnarray*} | \begin{eqnarray*} y_{t-k} - \nu & = & \psi_{0} \\ y_{t-k + 1} - \nu & = & \psi_{1} \\ y_{t-k+2} - \nu & = & \psi_{2} \\ \vdots & \vdots & \vdots \\ y_{t} & = & \psi_{k} \end{eqnarray*} |
| (1) | Chapter 9, p. 342, first displayed equation |
|---|
| \[ \begin{eqnarray*} \left[ \begin{array}{c} y_{1t} \\ y_{2t} \\ \vdots \\ y_{nt} \\ \end{array} \right] & = & \left[ \begin{array}{c} \nu_1 \\ \nu_2 \\ \vdots \\ \nu_n \\ \end{array} \right] + \left[ \begin{array}{cccc} p_{11} & 0 & \cdots & 0 \\ p_{21} & p_{22} & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ p_{n1} & p_{n2} & \cdots & p_{nn} \\ \end{array} \right] \left[ \begin{array}{c} v_{1t} \\ v_{2t} \\ \vdots \\ v_{nt} \\ \end{array} \right] \\ & + & \left[ \begin{array}{cccc} \xi_{1,11} & \xi_{1,21} & \cdots & \xi_{1,n1} \\ \xi_{1,21} & \xi_{1,22} & \cdots & \xi_{1,n2} \\ \vdots & \vdots & \ddots & \vdots \\ \xi_{1,n1} & \xi_{1,n2} & \cdots & \xi_{1,nn} \\ \end{array} \right] \left[ \begin{array}{c} v_{1,t-1} \\ v_{2,t-1} \\ \vdots \\ v_{n,t-1} \\ \end{array} \right] \\ & + & \left[ \begin{array}{cccc} \xi_{2,11} & \xi_{2,21} & \cdots & \xi_{2,n1} \\ \xi_{2,21} & \xi_{2,22} & \cdots & \xi_{2,n2} \\ \vdots & \vdots & \ddots & \vdots \\ \xi_{2,n1} & \xi_{2,n2} & \cdots & \xi_{2,nn} \\ \end{array} \right] \left[ \begin{array}{c} v_{1,t-2} \\ v_{2,t-2} \\ \vdots \\ v_{n,t-2} \\ \end{array} \right] + \cdots \\ \end{eqnarray*} \] | \[ \begin{eqnarray*} \left[ \begin{array}{c} y_{1t} \\ y_{2t} \\ \vdots \\ y_{nt} \\ \end{array} \right] & = & \left[ \begin{array}{c} \nu_1 \\ \nu_2 \\ \vdots \\ \nu_n \\ \end{array} \right] + \left[ \begin{array}{cccc} p_{11} & 0 & \cdots & 0 \\ p_{21} & p_{22} & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ p_{n1} & p_{n2} & \cdots & p_{nn} \\ \end{array} \right] \left[ \begin{array}{c} v_{1t} \\ v_{2t} \\ \vdots \\ v_{nt} \\ \end{array} \right] \\ & + & \left[ \begin{array}{cccc} \xi_{1,11} & \xi_{1,12} & \cdots & \xi_{1,1n} \\ \xi_{1,21} & \xi_{1,22} & \cdots & \xi_{1,2n} \\ \vdots & \vdots & \ddots & \vdots \\ \xi_{1,n1} & \xi_{1,n2} & \cdots & \xi_{1,nn} \\ \end{array} \right] \left[ \begin{array}{c} v_{1,t-1} \\ v_{2,t-1} \\ \vdots \\ v_{n,t-1} \\ \end{array} \right] \\ & + & \left[ \begin{array}{cccc} \xi_{2,11} & \xi_{2,12} & \cdots & \xi_{2,1n} \\ \xi_{2,21} & \xi_{2,22} & \cdots & \xi_{2,2n} \\ \vdots & \vdots & \ddots & \vdots \\ \xi_{2,n1} & \xi_{2,n2} & \cdots & \xi_{2,nn} \\ \end{array} \right] \left[ \begin{array}{c} v_{1,t-2} \\ v_{2,t-2} \\ \vdots \\ v_{n,t-2} \\ \end{array} \right] + \cdots \\ \end{eqnarray*} \] |
| (1) | Chapter 9, p. 342, sentence after displayed equation |
|---|
| Remember that \(\boldsymbol{\Xi}_i\equiv\boldsymbol{\Phi}_i{\bf P}\) and \(\boldsymbol{\Phi}_0\equiv{\bf I}_n\). | Remember that \(\boldsymbol{\Xi}_i\equiv\boldsymbol{\Psi}_i{\bf P}\) and \(\boldsymbol{\Psi}_0\equiv{\bf I}_n\). |
| (1) | Chapter 9, p. 342, third sentence of second paragraph |
|---|
| In period \(t+1\), \(y_{1,t+1}\) increases by \(\xi_{1,21}\) units, \(y_{2,t+1}\) increases by \(\xi_{1,22}\) units, \(y_{3,t+1}\) increases by \(\xi_{1,23}\) units, and so on. | In period \(t+1\), \(y_{1,t+1}\) increases by \(\xi_{1,12}\) units, \(y_{2,t+1}\) increases by \(\xi_{1,22}\) units, \(y_{3,t+1}\) increases by \(\xi_{1,32}\) units, and so on. |
| (1) | Chapter 9, p. 351, third sentence of second paragraph |
|---|
| After 12-quarters, ... inflation and unemployment equations. | After 12-quarters, ... inflation and funds equations. |
| (1) | Chapter 9, p. 354, first displayed equation |
|---|
| \[ \xi_{0,ij} (=p_{ij}), \xi{1,ij}, \xi{2,ij}, \ldots \] | \[ \xi_{0,ij} (=p_{ij}), \xi_{1,ij}, \xi_{2,ij}, \ldots \] |